梯形中位线定理是什么 直角梯形中位线怎么证明?
来源:太平洋焦点网 时间:2023-06-21 11:09:20
梯形中位线定理是什么
连接梯形两腰中点的线段叫做梯形的中位线。定理“梯形的中位线等于梯形的两底和的一半”叫做梯形中位线定理。这个定理的证明思路是将四边形问题转化成三角形问题来解决。方法:添加辅助线,如:将最左端上底顶点与最右端中位线端点连结并延长交下底的延长线于一点。这样原中位线就成了所构成的三角形的中位线了。容易证明,这时三角形的底长正好等于梯形两底的和。
根据三角形中位线定理可知这条中位线等于三角形底的一半。这样就证明了梯形中位线定理。

直角梯形中位线怎么证明
用向量法证明梯形中位线平行两边 向量AB//向量DC E,F分别为AD,BC中点求证:EF//AB//DC证明:向量EF=向量EA+向量AB+向量BF (1)式向量DC=向量DA+向量AB+向量BC (2)式 2向量EF+向量DA+向量AB+向量BC=向量DC+2向量EA+2向量AB+2向量BF 2向量EF=向量DC+向.
-
 微动态丨双柱式举升机有哪几种类型?双柱式举升机要注意什么? 双柱式举升机有哪几种类型?双柱式举升机有对称式和非对称式两种。对
微动态丨双柱式举升机有哪几种类型?双柱式举升机要注意什么? 双柱式举升机有哪几种类型?双柱式举升机有对称式和非对称式两种。对 -
 梯形中位线定理是什么 直角梯形中位线怎么证明? 梯形中位线定理是什么连接梯形两腰中点的线段叫做梯形的中位线。定理梯形的中位线等于梯形的两底和的一半叫做梯形中位线定理。这个定理的证
梯形中位线定理是什么 直角梯形中位线怎么证明? 梯形中位线定理是什么连接梯形两腰中点的线段叫做梯形的中位线。定理梯形的中位线等于梯形的两底和的一半叫做梯形中位线定理。这个定理的证 -
 缅北是属于哪个国家 缅甸北部本地人不害怕吗? 缅北是属于哪个国家缅北,位于缅甸的北部,与中国的德宏州,怒江州,以及临沧地区为邻。是属于缅甸管辖下的几个自治区。也叫邦,比如佤邦,
缅北是属于哪个国家 缅甸北部本地人不害怕吗? 缅北是属于哪个国家缅北,位于缅甸的北部,与中国的德宏州,怒江州,以及临沧地区为邻。是属于缅甸管辖下的几个自治区。也叫邦,比如佤邦, -
 环球视点!可续期公司债券的发行条件是什么?公司债券交易场地在哪? 可续期公司债券的发行条件是什么?公开发行公司债券,应当符合下列条
环球视点!可续期公司债券的发行条件是什么?公司债券交易场地在哪? 可续期公司债券的发行条件是什么?公开发行公司债券,应当符合下列条 -
 世界最资讯丨H股怎么交易?H股和港股有什么区别?s股是境外上市外资股吗? H股怎么交易?1 客户可以到香港任何一家银行或证券行开设香港股账户
世界最资讯丨H股怎么交易?H股和港股有什么区别?s股是境外上市外资股吗? H股怎么交易?1 客户可以到香港任何一家银行或证券行开设香港股账户 -
 新县吴陈河镇:四聚焦四落实做好“进家门、暖心门”大排查、大走访活动 为全面贯彻落实党的二十大精神,立足解决一批当前发展所需、改革所急、
新县吴陈河镇:四聚焦四落实做好“进家门、暖心门”大排查、大走访活动 为全面贯彻落实党的二十大精神,立足解决一批当前发展所需、改革所急、
-
 梯形中位线定理是什么 直角梯形中位线怎么证明? 梯形中位线定理是什么连接梯形两腰中点的线段叫做梯形的中位线。定理梯形的中位线等于梯形的两底和的一半叫做梯形中位线定理。这个定理的证
梯形中位线定理是什么 直角梯形中位线怎么证明? 梯形中位线定理是什么连接梯形两腰中点的线段叫做梯形的中位线。定理梯形的中位线等于梯形的两底和的一半叫做梯形中位线定理。这个定理的证 -
 清偿合伙人债务的法律方法是什么?合伙企业债务清偿的顺序是什么? 一、清偿合伙人债务的法律方法合伙的债务应当先用合伙财产进行偿还,合伙财产不能偿还,由合伙人偿还。《民法典》规定,合伙人对合伙债务承
清偿合伙人债务的法律方法是什么?合伙企业债务清偿的顺序是什么? 一、清偿合伙人债务的法律方法合伙的债务应当先用合伙财产进行偿还,合伙财产不能偿还,由合伙人偿还。《民法典》规定,合伙人对合伙债务承 -
 缅北是属于哪个国家 缅甸北部本地人不害怕吗? 缅北是属于哪个国家缅北,位于缅甸的北部,与中国的德宏州,怒江州,以及临沧地区为邻。是属于缅甸管辖下的几个自治区。也叫邦,比如佤邦,
缅北是属于哪个国家 缅甸北部本地人不害怕吗? 缅北是属于哪个国家缅北,位于缅甸的北部,与中国的德宏州,怒江州,以及临沧地区为邻。是属于缅甸管辖下的几个自治区。也叫邦,比如佤邦, -
 解决合伙人债务的合法途径是什么?合伙人的债务承担的范围是多大? 一、解决合伙人债务的合法途径解决合伙人债务的合法途径有:协商、调解、仲裁或者诉讼等,当事人如果要提起诉讼,需要注意原告要与本案有直
解决合伙人债务的合法途径是什么?合伙人的债务承担的范围是多大? 一、解决合伙人债务的合法途径解决合伙人债务的合法途径有:协商、调解、仲裁或者诉讼等,当事人如果要提起诉讼,需要注意原告要与本案有直 -
 企业工商注销网上操作流程是什么?企业工商注销的原因是什么? 一、企业工商注销网上操作流程企业工商注销网上操作流程为:1 登录电子税务局,点击清税注销税(费)申报及缴纳套餐菜单,进入公司注销登记引
企业工商注销网上操作流程是什么?企业工商注销的原因是什么? 一、企业工商注销网上操作流程企业工商注销网上操作流程为:1 登录电子税务局,点击清税注销税(费)申报及缴纳套餐菜单,进入公司注销登记引 -
 第十八届东明西瓜节与“瓜皮仔”形象授权签约仪式圆满完成,双方携手共创农业文创... 6月19日,第十八届东明西瓜节与知名网络动漫形象瓜皮仔形象授权签约仪式在山东省东明县小井镇圆满落幕。本次签约仪式旨在推动东明县小井镇
第十八届东明西瓜节与“瓜皮仔”形象授权签约仪式圆满完成,双方携手共创农业文创... 6月19日,第十八届东明西瓜节与知名网络动漫形象瓜皮仔形象授权签约仪式在山东省东明县小井镇圆满落幕。本次签约仪式旨在推动东明县小井镇 -
 普通合伙企业的债务承担规则是什么?合伙企业停业如何解除合同? 一、普通合伙企业的债务承担规则是什么1 遵循双重优先权原则。 对于合伙人而言,如果个人债务与合伙债务并存,原则上应当适用双重优先权原
普通合伙企业的债务承担规则是什么?合伙企业停业如何解除合同? 一、普通合伙企业的债务承担规则是什么1 遵循双重优先权原则。 对于合伙人而言,如果个人债务与合伙债务并存,原则上应当适用双重优先权原 -
 合伙债务清偿的应对措施是什么?合伙债务纠纷如何进行? 一、合伙债务清偿的应对措施合伙人清偿合伙企业的债务的方法:先由合伙企业以其全部财产来清偿债务;如果合伙企业的财产不足以清偿全部债务
合伙债务清偿的应对措施是什么?合伙债务纠纷如何进行? 一、合伙债务清偿的应对措施合伙人清偿合伙企业的债务的方法:先由合伙企业以其全部财产来清偿债务;如果合伙企业的财产不足以清偿全部债务 -
 合伙协议纠纷案件的解决策略是什么?合伙协议纠纷案件有哪几种类型? 一、合伙协议纠纷案件的解决策略合伙协议纠纷案件的解决策略如下:1 协商解决;2 通过第三者调解解决;3 申请仲裁。不愿通过协商、调解解决或
合伙协议纠纷案件的解决策略是什么?合伙协议纠纷案件有哪几种类型? 一、合伙协议纠纷案件的解决策略合伙协议纠纷案件的解决策略如下:1 协商解决;2 通过第三者调解解决;3 申请仲裁。不愿通过协商、调解解决或 -
 苹果手机如何添加加密门禁?nfc门禁卡苹果手机怎么使用? 苹果手机如何添加加密门禁?苹果手机增加加密访问控制方法;方法 步骤
苹果手机如何添加加密门禁?nfc门禁卡苹果手机怎么使用? 苹果手机如何添加加密门禁?苹果手机增加加密访问控制方法;方法 步骤 -
 【环球新视野】英雄联盟山海绘卷剑魔什么时候上线?英雄联盟山海绘卷是限定吗? 英雄联盟山海绘卷剑魔什么时候上线?山海绘卷剑魔将在4 3版本6月21日
【环球新视野】英雄联盟山海绘卷剑魔什么时候上线?英雄联盟山海绘卷是限定吗? 英雄联盟山海绘卷剑魔什么时候上线?山海绘卷剑魔将在4 3版本6月21日 -
 环球精选!Win10火炬之光2没有声音怎么办? 火炬之光无限震动怎么关闭? Win10火炬之光2没有声音怎么办?Win10火炬之光2没声音的解决方法1、
环球精选!Win10火炬之光2没有声音怎么办? 火炬之光无限震动怎么关闭? Win10火炬之光2没有声音怎么办?Win10火炬之光2没声音的解决方法1、 -
 弹力包括哪些力?弹簧弹力的方向怎么判断?_全球讯息 弹力包括哪些力?弹力有支持力、拉力、压力。物体受外力作用发生形变
弹力包括哪些力?弹簧弹力的方向怎么判断?_全球讯息 弹力包括哪些力?弹力有支持力、拉力、压力。物体受外力作用发生形变 -
 中国足球出线是什么意思?足球中出线是什么意思? 环球视点 中国足球出线是什么意思?2018年的俄罗斯世界杯,中国队是没有取得出
中国足球出线是什么意思?足球中出线是什么意思? 环球视点 中国足球出线是什么意思?2018年的俄罗斯世界杯,中国队是没有取得出 -
 宽带速率1000m下载速度有多少?宽带速率1000m怎么理解?-环球观速讯 宽带速率1000m下载速度有多少?演示工具:电脑型号:华硕adolbook14
宽带速率1000m下载速度有多少?宽带速率1000m怎么理解?-环球观速讯 宽带速率1000m下载速度有多少?演示工具:电脑型号:华硕adolbook14 -
 vivo手机怎么备份到电脑?vivo x9如何备份使用云服务? vivo手机怎么备份到电脑?Vivo手机备份手机数据到电脑方法:将手机连
vivo手机怎么备份到电脑?vivo x9如何备份使用云服务? vivo手机怎么备份到电脑?Vivo手机备份手机数据到电脑方法:将手机连 -
 合伙人债务清偿的相关法律规定是什么?合伙债务纠纷的诉讼时效是多久? 一、合伙人债务清偿的相关法律规定合伙人债务清偿的相关法律规定为:《中华人民共和国民法典》第九百七十三条 【合伙人的连带责任及追偿权
合伙人债务清偿的相关法律规定是什么?合伙债务纠纷的诉讼时效是多久? 一、合伙人债务清偿的相关法律规定合伙人债务清偿的相关法律规定为:《中华人民共和国民法典》第九百七十三条 【合伙人的连带责任及追偿权 -
 安培定律是什么?左手定则是安培定则吗? 安培定律是什么?安培定律是一个电磁定律,它表示电流和电流激发磁场
安培定律是什么?左手定则是安培定则吗? 安培定律是什么?安培定律是一个电磁定律,它表示电流和电流激发磁场 -
焦点精选!房贷和房产证必须写同一个人的名字吗?房产证为何女方的名字在前? 房贷和房产证必须写同一个人的名字吗?房贷的借款人的确要和房产证
-
 焦点报道:大连荧光海在哪个位置?大连荧光海滩几月份有? 大连荧光海在哪个位置这片神秘的荧光海就在大连,位于甘井子区的大黑
焦点报道:大连荧光海在哪个位置?大连荧光海滩几月份有? 大连荧光海在哪个位置这片神秘的荧光海就在大连,位于甘井子区的大黑 -
 【天天速看料】finalcutprox怎么制作led灯光效果的文字动画?finalcutprox静帧时长怎么设置? finalcutprox怎么制作led灯光效果的文字动画?1、左边点T,左边点击
【天天速看料】finalcutprox怎么制作led灯光效果的文字动画?finalcutprox静帧时长怎么设置? finalcutprox怎么制作led灯光效果的文字动画?1、左边点T,左边点击 -
 环球快看点丨LOL沙漠死神出装怎么搭配?英雄联盟沙漠死神如何出装? LOL沙漠死神出装怎么搭配?LOL狗头最强出装1、核心装备正常情况下,
环球快看点丨LOL沙漠死神出装怎么搭配?英雄联盟沙漠死神如何出装? LOL沙漠死神出装怎么搭配?LOL狗头最强出装1、核心装备正常情况下, -
 餐饮管理公司注册流程是什么?公司注册资本多少比较合适? 一、餐饮管理公司注册流程餐饮管理公司注册流程如下:1 准备公司名称到工商局核名;2 到刻章厂刻章一套分为公章、财务章、法人章、合同章;3
餐饮管理公司注册流程是什么?公司注册资本多少比较合适? 一、餐饮管理公司注册流程餐饮管理公司注册流程如下:1 准备公司名称到工商局核名;2 到刻章厂刻章一套分为公章、财务章、法人章、合同章;3 -
 变更营业执照法人需要本人去吗?变更营业执照的程序是什么? 一、变更营业执照法人需要本人去吗变更营业执照法人一般需要本人去。当然有授权委托书也可以委托他人办理,可以由公司员工带相应的材料到工
变更营业执照法人需要本人去吗?变更营业执照的程序是什么? 一、变更营业执照法人需要本人去吗变更营业执照法人一般需要本人去。当然有授权委托书也可以委托他人办理,可以由公司员工带相应的材料到工 -
 环球今头条!造价工程师挂靠费多少?造价工程师合格线是多少? 造价工程师挂靠费多少?建设部造价工程师4-5万 年(带高工4 5-6万 年)
环球今头条!造价工程师挂靠费多少?造价工程师合格线是多少? 造价工程师挂靠费多少?建设部造价工程师4-5万 年(带高工4 5-6万 年) -
 公司开基本户需要哪些资料?开基本户的程序是什么? 一、公司开基本户需要哪些资料公司开基本户需要以下资料:1 公司营业执照:需要提供公司营业执照原件和复印件;2 公司章程:需要提供公司章
公司开基本户需要哪些资料?开基本户的程序是什么? 一、公司开基本户需要哪些资料公司开基本户需要以下资料:1 公司营业执照:需要提供公司营业执照原件和复印件;2 公司章程:需要提供公司章 -
 天天观察:河北承德特色水果都有什么?盘点四个承德特色水果 河北承德特色水果有兴隆山楂、兴隆苹果、兴隆柿子、隆化山杏、承德
天天观察:河北承德特色水果都有什么?盘点四个承德特色水果 河北承德特色水果有兴隆山楂、兴隆苹果、兴隆柿子、隆化山杏、承德 -
 天天热议:新蔡县司法局陈店司法所:土地纠纷多反复 调解帮忙迎刃解 张某与杨某系新蔡县陈店镇黄园村委的村民,张某家种植两家责任田毗邻,
天天热议:新蔡县司法局陈店司法所:土地纠纷多反复 调解帮忙迎刃解 张某与杨某系新蔡县陈店镇黄园村委的村民,张某家种植两家责任田毗邻, -
 亚洲足球排名前十名的国家是哪些?2023年澳网决赛什么时间开始? 亚洲足球排名前十名的国家是哪些?据2023年最新的亚洲足球排名榜显示
亚洲足球排名前十名的国家是哪些?2023年澳网决赛什么时间开始? 亚洲足球排名前十名的国家是哪些?据2023年最新的亚洲足球排名榜显示 -
 合同制算编外人员吗?事业单位编制的考取条件是什么? 一、合同制算编外人员吗合同制算编外人员。编外人员也就是不在单位编制内,但是其与单位的劳动关系是存在的。因此经双方协商一致,可以签订
合同制算编外人员吗?事业单位编制的考取条件是什么? 一、合同制算编外人员吗合同制算编外人员。编外人员也就是不在单位编制内,但是其与单位的劳动关系是存在的。因此经双方协商一致,可以签订 -
 天天短讯!心脏支架有没有年限?心脏支架术后注意什么事项? 心脏支架没有年限,这个问题应该从心脏病的病因来考虑。为什么要给
天天短讯!心脏支架有没有年限?心脏支架术后注意什么事项? 心脏支架没有年限,这个问题应该从心脏病的病因来考虑。为什么要给 -
 处理交通事故的注意事项有哪些?单方交通事故责任认定书有什么用? 单方事故需要交警做出事故认定责任书当作交通事故的证据,交通事故
处理交通事故的注意事项有哪些?单方交通事故责任认定书有什么用? 单方事故需要交警做出事故认定责任书当作交通事故的证据,交通事故 -
 汝南邮政:培训加演练 消防更安全-今日讯 为强化安全管理、夯实安全基础,消除和遏制各类消防安全隐患,6月20日
汝南邮政:培训加演练 消防更安全-今日讯 为强化安全管理、夯实安全基础,消除和遏制各类消防安全隐患,6月20日 -
 信息:如何申请水滴筹?水滴筹怎么操作? 如何申请水滴筹?水滴筹怎么操作?申请水滴筹的方法一般有两种,要
信息:如何申请水滴筹?水滴筹怎么操作? 如何申请水滴筹?水滴筹怎么操作?申请水滴筹的方法一般有两种,要 -
 Pages文稿怎么快速设计一款证书?pages文稿字符间距怎么设置?-天天即时 Pages文稿怎么快速设计一款证书?1、首先打开电脑的"启动台",然后打
Pages文稿怎么快速设计一款证书?pages文稿字符间距怎么设置?-天天即时 Pages文稿怎么快速设计一款证书?1、首先打开电脑的"启动台",然后打 -
 工业空调日常怎么维护保养?家用空调和工业用空调有什么区别? 世界新要闻 工业空调日常怎么维护保养?1 、节能环保空调机控制器的操作:当气
工业空调日常怎么维护保养?家用空调和工业用空调有什么区别? 世界新要闻 工业空调日常怎么维护保养?1 、节能环保空调机控制器的操作:当气 -
 箭牌家居:让智能带有温度是我们一直在思考的课题 纵观近几年卫浴市场的发展变化,消费升级、高颜值、健康、智能成为了行业的主要方向。6月7日,以智净美好 惬意空间 为主题的2023中国智能
箭牌家居:让智能带有温度是我们一直在思考的课题 纵观近几年卫浴市场的发展变化,消费升级、高颜值、健康、智能成为了行业的主要方向。6月7日,以智净美好 惬意空间 为主题的2023中国智能 -
 goodnotes怎么设置封面?goodnotes怎么共享笔记? goodnotes封面设置教程1、选择一个笔记本2、点击右上角的三个点3、
goodnotes怎么设置封面?goodnotes怎么共享笔记? goodnotes封面设置教程1、选择一个笔记本2、点击右上角的三个点3、 -
 全球百事通!dnf恋之独角兽如何获得?dnf小魔女的偏爱怎么选择偏爱对象? dnf恋之独角兽如何获得?可以通过100个金牌在卡妮娜处兑换。金牌的获
全球百事通!dnf恋之独角兽如何获得?dnf小魔女的偏爱怎么选择偏爱对象? dnf恋之独角兽如何获得?可以通过100个金牌在卡妮娜处兑换。金牌的获 -
 速递!iphone13用的什么屏幕?iphone13怎么强制重启手机? iphone13用的什么屏幕?iphone13采用6 1英寸OLED屏幕,机身尺寸高度
速递!iphone13用的什么屏幕?iphone13怎么强制重启手机? iphone13用的什么屏幕?iphone13采用6 1英寸OLED屏幕,机身尺寸高度 -
 NVIDIAA100玩游戏会怎么样?你想体验一下吗? 30万元的NVIDIAA100,用它玩游戏会怎么样?AI浪潮之下,NVIDIA A100
NVIDIAA100玩游戏会怎么样?你想体验一下吗? 30万元的NVIDIAA100,用它玩游戏会怎么样?AI浪潮之下,NVIDIA A100 -
 焦点精选!中华人民共和国民法典第一千零五十一条是什么内容?有哪些情形婚姻无效? 现在18岁是不可以领结婚证的。国家规定结婚年龄:男不得早于二十二
焦点精选!中华人民共和国民法典第一千零五十一条是什么内容?有哪些情形婚姻无效? 现在18岁是不可以领结婚证的。国家规定结婚年龄:男不得早于二十二 -
 河北保定特产有哪些?保定的特色小吃是什么? 保定的特色小吃有驴肉火烧、白运章包子、白肉罩火烧、元宵王、牛肉
河北保定特产有哪些?保定的特色小吃是什么? 保定的特色小吃有驴肉火烧、白运章包子、白肉罩火烧、元宵王、牛肉 -
 持股比例多少算控股?大股东增持股票会涨吗? 一、持股比例多少算控股持股比例50%算控股。《中华人民共和国公司法》 第二百一十六条本法下列用语的含义:(一)高级管理人员,是指公司的
持股比例多少算控股?大股东增持股票会涨吗? 一、持股比例多少算控股持股比例50%算控股。《中华人民共和国公司法》 第二百一十六条本法下列用语的含义:(一)高级管理人员,是指公司的 -
 简易公司注销要多久?公司简易注销的条件是什么? 一、简易公司注销要多久简易公司注销要48天左右。1 公司简易注销的的公告时间一般为三个月,具体就是45天左右。2 公告期之后就会到政府办理
简易公司注销要多久?公司简易注销的条件是什么? 一、简易公司注销要多久简易公司注销要48天左右。1 公司简易注销的的公告时间一般为三个月,具体就是45天左右。2 公告期之后就会到政府办理 -
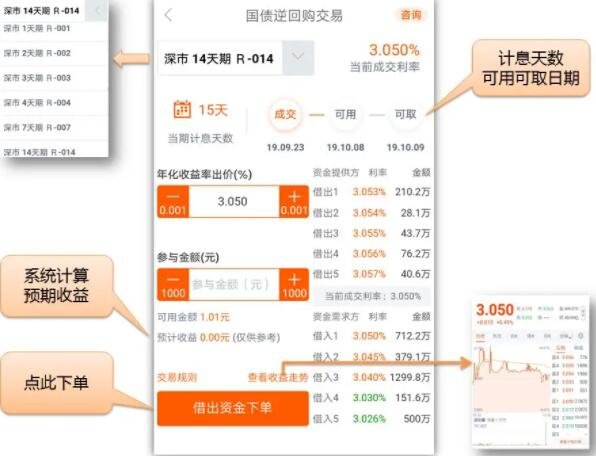 国债逆回购操作流程是什么介绍 国债逆回购的基础知识汇总_环球快消息 国债逆回购操作流程是什么介绍虽然每个证券公司的交易界面不一样,
国债逆回购操作流程是什么介绍 国债逆回购的基础知识汇总_环球快消息 国债逆回购操作流程是什么介绍虽然每个证券公司的交易界面不一样, -
 淮南有哪些特色小吃? 安徽淮南特产有哪些? 淮南的特色小吃有八公山豆腐、驻马店羊肉汤、寿县大救驾、淮南馓子
淮南有哪些特色小吃? 安徽淮南特产有哪些? 淮南的特色小吃有八公山豆腐、驻马店羊肉汤、寿县大救驾、淮南馓子 -
 魔兽怀旧服暮光预言者在哪?暮光预言者巡逻路线是什么? 魔兽怀旧服暮光预言者在哪?魔兽怀旧服暮光预言者位置:魔兽怀旧服暮
魔兽怀旧服暮光预言者在哪?暮光预言者巡逻路线是什么? 魔兽怀旧服暮光预言者在哪?魔兽怀旧服暮光预言者位置:魔兽怀旧服暮 -
 公司的法定代表人是什么职务?公司法人跟法定代表人有什么区别? 一、公司的法定代表人是什么职务公司的法定代表人一般为董事长,法定代表人是指依法代表法人行使民事权利,履行民事义务的主要负责人(如:
公司的法定代表人是什么职务?公司法人跟法定代表人有什么区别? 一、公司的法定代表人是什么职务公司的法定代表人一般为董事长,法定代表人是指依法代表法人行使民事权利,履行民事义务的主要负责人(如: -
 全球今日报丨蛋仔派对桃花币如何获得?蛋仔派对蛋币怎么获得? 蛋仔派对桃花币如何获得?收集桃花:玩家通过游戏内活动获取桃花奖励
全球今日报丨蛋仔派对桃花币如何获得?蛋仔派对蛋币怎么获得? 蛋仔派对桃花币如何获得?收集桃花:玩家通过游戏内活动获取桃花奖励
热门资讯
-
 第十八届东明西瓜节与“瓜皮仔”形象授权签约仪式圆满完成,双方携手共创农业文创... 6月19日,第十八届东明西瓜节与知...
第十八届东明西瓜节与“瓜皮仔”形象授权签约仪式圆满完成,双方携手共创农业文创... 6月19日,第十八届东明西瓜节与知... -
 goodnotes怎么设置封面?goodnotes怎么共享笔记? goodnotes封面设置教程1、选择一个...
goodnotes怎么设置封面?goodnotes怎么共享笔记? goodnotes封面设置教程1、选择一个... -
 如何申请水滴筹?水滴筹怎么申请? 如何申请水滴筹?水滴筹怎么申请...
如何申请水滴筹?水滴筹怎么申请? 如何申请水滴筹?水滴筹怎么申请... -
 当前热讯:中秋节放假安排介绍 2022年中秋节股市安排简介 中秋节放假安排介绍2022年中秋节放...
当前热讯:中秋节放假安排介绍 2022年中秋节股市安排简介 中秋节放假安排介绍2022年中秋节放...
观察
图片新闻
-
 信用卡逾期不还会坐牢吗?信用卡逾期警察上门抓人是真的吗? 信用卡逾期不还会坐牢吗?信用卡不...
信用卡逾期不还会坐牢吗?信用卡逾期警察上门抓人是真的吗? 信用卡逾期不还会坐牢吗?信用卡不... -
 什么是医保?无登记的参保信息怎么解决? 什么是医保?医保指社会医疗保险,...
什么是医保?无登记的参保信息怎么解决? 什么是医保?医保指社会医疗保险,... -
 今日热议:新时代三亚好少年、三亚市第九小学学生葛蕃宁:敏而好学的阳光男儿 葛蕃宁参加红色经典诵读比赛,葛蕃...
今日热议:新时代三亚好少年、三亚市第九小学学生葛蕃宁:敏而好学的阳光男儿 葛蕃宁参加红色经典诵读比赛,葛蕃... -
 王者荣耀版本更新失败怎么办?王者更新不了怎么解决? 王者荣耀版本更新失败怎么办?王者...
王者荣耀版本更新失败怎么办?王者更新不了怎么解决? 王者荣耀版本更新失败怎么办?王者...
精彩新闻
-
 平安短期综合意外险怎么样?员工意外保险一年多少钱? 平安短期综合意外险怎么样?总体来...
平安短期综合意外险怎么样?员工意外保险一年多少钱? 平安短期综合意外险怎么样?总体来... -
 贷款逾期后的合法处置方法是什么?贷款逾期诉讼时效是多久? 一、贷款逾期后的合法处置方法贷款...
贷款逾期后的合法处置方法是什么?贷款逾期诉讼时效是多久? 一、贷款逾期后的合法处置方法贷款... -
 今日观点!身份证掉了被人拿去贷款怎么办?已经被注销的身份证欠网贷? 身份证掉了被人拿去贷款怎么办?身...
今日观点!身份证掉了被人拿去贷款怎么办?已经被注销的身份证欠网贷? 身份证掉了被人拿去贷款怎么办?身... -
 梵净山看日出什么时候去最好?梵净山几月份去最好? 梵净山看日出什么时候去最好?春天(...
梵净山看日出什么时候去最好?梵净山几月份去最好? 梵净山看日出什么时候去最好?春天(... -
 2022年即将倒闭的银行有哪些?不允许倒闭的六大银行都有谁? 2022年即将倒闭的银行有哪些?第一...
2022年即将倒闭的银行有哪些?不允许倒闭的六大银行都有谁? 2022年即将倒闭的银行有哪些?第一... -
 银行储蓄的方式有哪些? 银行的利息需要缴纳个人所得税吗? 当前快报 银行储蓄的方式有哪些?1 活期储蓄...
银行储蓄的方式有哪些? 银行的利息需要缴纳个人所得税吗? 当前快报 银行储蓄的方式有哪些?1 活期储蓄... -
 每日动态!西施姓什么 西施的结局是什么? 西施姓什么西施,子姓施氏,本名施...
每日动态!西施姓什么 西施的结局是什么? 西施姓什么西施,子姓施氏,本名施... -
 网贷还款出现问题如何解决?网贷诉讼时效是多久? 一、网贷还款出现问题如何解决网贷...
网贷还款出现问题如何解决?网贷诉讼时效是多久? 一、网贷还款出现问题如何解决网贷... -
 微动态丨双柱式举升机有哪几种类型?双柱式举升机要注意什么? 双柱式举升机有哪几种类型?双柱式...
微动态丨双柱式举升机有哪几种类型?双柱式举升机要注意什么? 双柱式举升机有哪几种类型?双柱式... -
 关于公司注销后债权债务的处理方法是什么? 一、关于公司注销后债权债务的处理...
关于公司注销后债权债务的处理方法是什么? 一、关于公司注销后债权债务的处理... -
 ibm笔记本如何一键还原? thinkpad怎么恢复系统? ibm笔记本如何一键还原?检测一键还...
ibm笔记本如何一键还原? thinkpad怎么恢复系统? ibm笔记本如何一键还原?检测一键还... -
 当前热讯:中秋节放假安排介绍 2022年中秋节股市安排简介 中秋节放假安排介绍2022年中秋节放...
当前热讯:中秋节放假安排介绍 2022年中秋节股市安排简介 中秋节放假安排介绍2022年中秋节放... -
 短期债券具有什么优点?短期债券具有什么弊端? 全球独家 短期债券具有什么优点?安全性较高...
短期债券具有什么优点?短期债券具有什么弊端? 全球独家 短期债券具有什么优点?安全性较高... -
 股东过世如何处理股权变更手续? 一、股东过世,如何处理股权变更手...
股东过世如何处理股权变更手续? 一、股东过世,如何处理股权变更手... -
 公司类型应如何填写?公司设立可以以劳务出资吗? 一、公司类型应如何填写企业类型根...
公司类型应如何填写?公司设立可以以劳务出资吗? 一、公司类型应如何填写企业类型根... - 世界简讯:体育传统项目有哪些方面?中国发明了哪些体育项目? 体育传统项目有哪些方面中国传统体...
-
 急性心肌梗塞的临床表现及并发症?急性心肌梗塞是什么原因造成的?_每日热闻 急性心肌梗塞(即急性心肌梗死)是临...
急性心肌梗塞的临床表现及并发症?急性心肌梗塞是什么原因造成的?_每日热闻 急性心肌梗塞(即急性心肌梗死)是临... -
 绿豆汤煮熟为什么会变成红色?绿豆汤变红还能喝吗? 绿豆汤煮熟为什么会变成红色?变红...
绿豆汤煮熟为什么会变成红色?绿豆汤变红还能喝吗? 绿豆汤煮熟为什么会变成红色?变红... -
 创业板股票怎么买卖?股票当天买当天可以卖吗? 创业板股票怎么买卖?创业板的股票...
创业板股票怎么买卖?股票当天买当天可以卖吗? 创业板股票怎么买卖?创业板的股票... -
 黑色曼陀罗有毒吗?黑色曼陀罗的花语和寓意是什么? 今日播报 黑色曼陀罗有毒吗?有毒黑色曼陀罗,...
黑色曼陀罗有毒吗?黑色曼陀罗的花语和寓意是什么? 今日播报 黑色曼陀罗有毒吗?有毒黑色曼陀罗,... -
 120级如何解锁德拉诺飞行?德拉诺如何学习飞行? 120级如何解锁德拉诺飞行?在魔兽世...
120级如何解锁德拉诺飞行?德拉诺如何学习飞行? 120级如何解锁德拉诺飞行?在魔兽世... -
 当前报道:乐天股票在哪里上市 股票买卖双方如何成交 乐天股票在哪里上市韩国证券交易所...
当前报道:乐天股票在哪里上市 股票买卖双方如何成交 乐天股票在哪里上市韩国证券交易所... -
 当前速读:56MW!内蒙古达拉特旗2023年分散式风电、分布式光伏项目优选结果公布 (资料图片)6月15日,内蒙古达拉特...
当前速读:56MW!内蒙古达拉特旗2023年分散式风电、分布式光伏项目优选结果公布 (资料图片)6月15日,内蒙古达拉特... -
 每日速讯:雪豹周卫国最后的结局是什么?雪豹周卫国和刘志辉是亲兄弟吗? 雪豹周卫国最后的结局是什么?《雪...
每日速讯:雪豹周卫国最后的结局是什么?雪豹周卫国和刘志辉是亲兄弟吗? 雪豹周卫国最后的结局是什么?《雪... -
 脱毛后以后还会长吗?脱毛时用不用避开生理期? 脱毛后以后还会长吗?脱毛仪是否能...
脱毛后以后还会长吗?脱毛时用不用避开生理期? 脱毛后以后还会长吗?脱毛仪是否能... -
 Sketch怎么进行一键替换颜色?sketch怎么裁剪图片一部分?-快资讯 Sketch怎么进行一键替换颜色?打开...
Sketch怎么进行一键替换颜色?sketch怎么裁剪图片一部分?-快资讯 Sketch怎么进行一键替换颜色?打开... -
 怎样进行股权收购?股权收购的方式有哪些? 一、怎样进行股权收购股权收购的方...
怎样进行股权收购?股权收购的方式有哪些? 一、怎样进行股权收购股权收购的方... -
 报道:Sketch怎么增加组件?Sketch文字怎么添加渐变色? Sketch怎么增加组件?打开电脑,找...
报道:Sketch怎么增加组件?Sketch文字怎么添加渐变色? Sketch怎么增加组件?打开电脑,找... -
 浮动盈亏是什么意思?什么叫浮动盈亏? 浮动盈亏是什么意思?什么叫浮动盈...
浮动盈亏是什么意思?什么叫浮动盈亏? 浮动盈亏是什么意思?什么叫浮动盈... -
 职工工会经费的具体使用方式是什么?工会经费能零申报吗? 1、《中小微型企业认定申报表》;2...
职工工会经费的具体使用方式是什么?工会经费能零申报吗? 1、《中小微型企业认定申报表》;2... -
 轴流风机的工作原理是什么?轴流风机怎么运行检查?_天天时讯 轴流风机的工作原理是什么?当叶轮...
轴流风机的工作原理是什么?轴流风机怎么运行检查?_天天时讯 轴流风机的工作原理是什么?当叶轮... -
 赵丽颖是儿子还是女儿?赵丽颖的老公? 赵丽颖是儿子还是女儿?儿子儿子。...
赵丽颖是儿子还是女儿?赵丽颖的老公? 赵丽颖是儿子还是女儿?儿子儿子。... -
 车道级定位是什么?如何下载北斗定位? 车道级定位是什么刘旭解释说:当司...
车道级定位是什么?如何下载北斗定位? 车道级定位是什么刘旭解释说:当司... -
 如何申请水滴筹?水滴筹怎么申请? 如何申请水滴筹?水滴筹怎么申请...
如何申请水滴筹?水滴筹怎么申请? 如何申请水滴筹?水滴筹怎么申请... -
 限制稀土出口的原因是什么?限制稀土出口给我国带来了什么影响? 环球快播 限制稀土出口的原因是什么?稀土非...
限制稀土出口的原因是什么?限制稀土出口给我国带来了什么影响? 环球快播 限制稀土出口的原因是什么?稀土非... -
 信用卡逾期不还会坐牢吗?信用卡逾期警察上门抓人是真的吗? 信用卡逾期不还会坐牢吗?信用卡不...
信用卡逾期不还会坐牢吗?信用卡逾期警察上门抓人是真的吗? 信用卡逾期不还会坐牢吗?信用卡不... -
 公司股东会必须具备哪些法律职责?公司股东会和董事会的区别是什么? 一、公司股东会必须具备哪些法律职...
公司股东会必须具备哪些法律职责?公司股东会和董事会的区别是什么? 一、公司股东会必须具备哪些法律职... -
 怎么给股票增加板块 板块补涨个股怎么选?-环球热点 怎么给股票增加板块你先选中后点右...
怎么给股票增加板块 板块补涨个股怎么选?-环球热点 怎么给股票增加板块你先选中后点右... -
 股票大量融资买入说明什么?股票融资买入增加是好是坏?|世界最资讯 股票的融资买入什么意思?股票融资...
股票大量融资买入说明什么?股票融资买入增加是好是坏?|世界最资讯 股票的融资买入什么意思?股票融资... -
 每日头条!新蔡县脱贫户监测对象收入预采集分析工作推进会召开 6月20日下午,新蔡县脱贫户监测对...
每日头条!新蔡县脱贫户监测对象收入预采集分析工作推进会召开 6月20日下午,新蔡县脱贫户监测对... -
 世界热消息:微信还有这么多隐藏功能吗?你知道如何使用吗? 微信除了发消息、朋友圈,还有5项...
世界热消息:微信还有这么多隐藏功能吗?你知道如何使用吗? 微信除了发消息、朋友圈,还有5项... -
 债券是资产还是负债?债券到期收益率怎么算? 环球消息 债券是资产还是负债?债券既可以被...
债券是资产还是负债?债券到期收益率怎么算? 环球消息 债券是资产还是负债?债券既可以被... -
 联通校招签约的都呆了多久?大学本科毕业去联通上班好吗?-环球观焦点 联通校招签约的都呆了多久?三年。...
联通校招签约的都呆了多久?大学本科毕业去联通上班好吗?-环球观焦点 联通校招签约的都呆了多久?三年。... -
 环乙酮是什么?环乙酮的作用是什么? 全球最资讯 环乙酮是什么?环己酮,是一种有机...
环乙酮是什么?环乙酮的作用是什么? 全球最资讯 环乙酮是什么?环己酮,是一种有机... -
 什么是负债整合? 负债整合的目标有哪些内容? 什么是负债整合?负债整合是将并购...
什么是负债整合? 负债整合的目标有哪些内容? 什么是负债整合?负债整合是将并购... -
 公积金销户未结算指的是什么?公积金销户未结算意味着什么 ?_天天报道 公积金销户未结算指的是什么?公积...
公积金销户未结算指的是什么?公积金销户未结算意味着什么 ?_天天报道 公积金销户未结算指的是什么?公积... -
 黄山的传统风味小吃是什么? 黄山特传统特色美食有哪些? 头条 黄山的特色小吃有徽州臭豆腐、黄豆...
黄山的传统风味小吃是什么? 黄山特传统特色美食有哪些? 头条 黄山的特色小吃有徽州臭豆腐、黄豆... -
 天天看点:龙生福瑞6号年金保险好处是什么?龙生福瑞6号年金保险要怎么买呢? 龙生福瑞6号年金保险好处是什么?1...
天天看点:龙生福瑞6号年金保险好处是什么?龙生福瑞6号年金保险要怎么买呢? 龙生福瑞6号年金保险好处是什么?1... -
 炎亚纶和三个男的是什么意思? 炎亚纶谈过恋爱吗?|天天新动态 炎亚纶和三个男的是什么意思?事情...
炎亚纶和三个男的是什么意思? 炎亚纶谈过恋爱吗?|天天新动态 炎亚纶和三个男的是什么意思?事情... -
 如何申请水滴筹?水滴筹申请步骤 如何申请水滴筹?申请水滴筹的方法...
如何申请水滴筹?水滴筹申请步骤 如何申请水滴筹?申请水滴筹的方法...